Concentration influences

A simple analytical description of the composition dependence of the viscosity of polymer solutions, covering the entire range from the pure solvent up to the pure melt or to the glass transition of the system, would of course be the ultimate goal. Such a task requires the modeling from isolated, more or less non-draining polymer coils to a fully developed entanglement network; it is therefore small wonder that the number of such models is overlookable. A phenomenological Ansatz[^326] [^337] (see the following chart) describes the real behavior surprisingly very well.

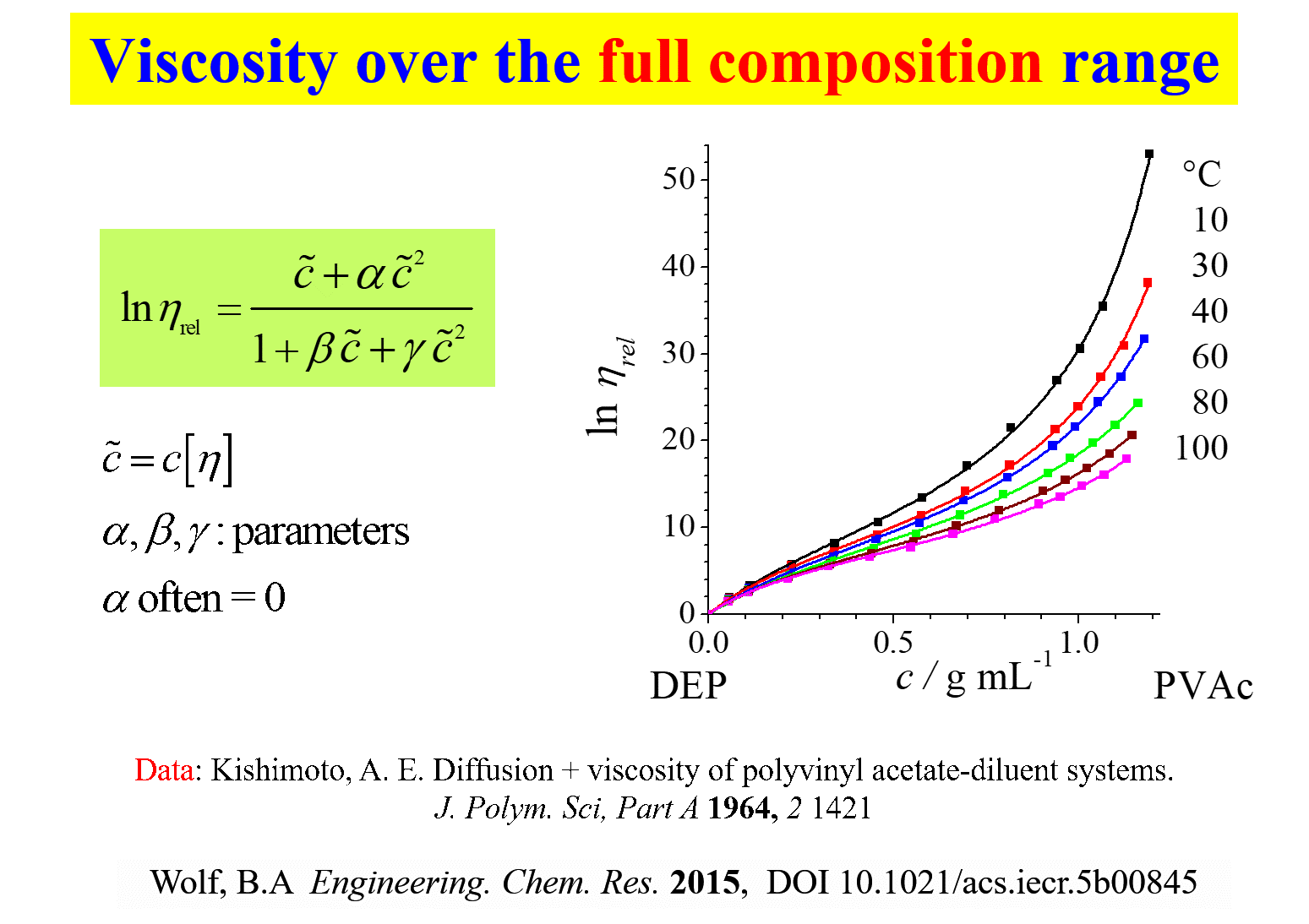
\({\eta _{{\rm{rel}}}}\) is the viscosity of the system, normalized to that of the pure solvent, \(\tilde c = c\left[ {\eta } \right]\) stands for the reduced polymer concentration, the product of c (mass/volume) and the intrinsic viscosity \(\left[ \eta \right]\) (volume/mass); \(\alpha\), \(\beta\) and \(\gamma\) are system specific parameters, where \(\alpha\) can in most cases be set zero. One important exception that requires \(\alpha\) concerns the modeling of polyelectrolyte solutions in the absence of extra salt.

As long as the viscosity represents an equation of state, its modeling is considerably facilitated by the following thermodynamically inspired approach.

In the present context the second term is the most interesting one. It introduces the generalized intrinsic viscosity \(\left\{ \eta \right\}\) as the relative change of \(\eta\) with polymer concentration c. For infinite dilution \(\left\{ \eta \right\}\) becomes identical with the usual intrinsic viscosity and - more importantly - its limiting value for the pure melt (c becoming identical with the density \(\rho\) of the polymer) yields a new valuable parameter, namely the intrinsic bulkiness[^337] \([\kern-0.15em[ \eta ]\kern-0.15em]\).

Combining the expression for \(\ln {\eta _{{\rm{rel}}}}\) as a function of c, introduced above, with the phenomenological thermodynamic dependencies provides access to a number of valuable characteristic data as outlined below.

The next chart presents some examples[^337] for the composition dependence of \(\left\{ \eta \right\}\) and compares \(\left[ \eta \right]\) and \([\kern-0.15em[ \eta ]\kern-0.15em]\).

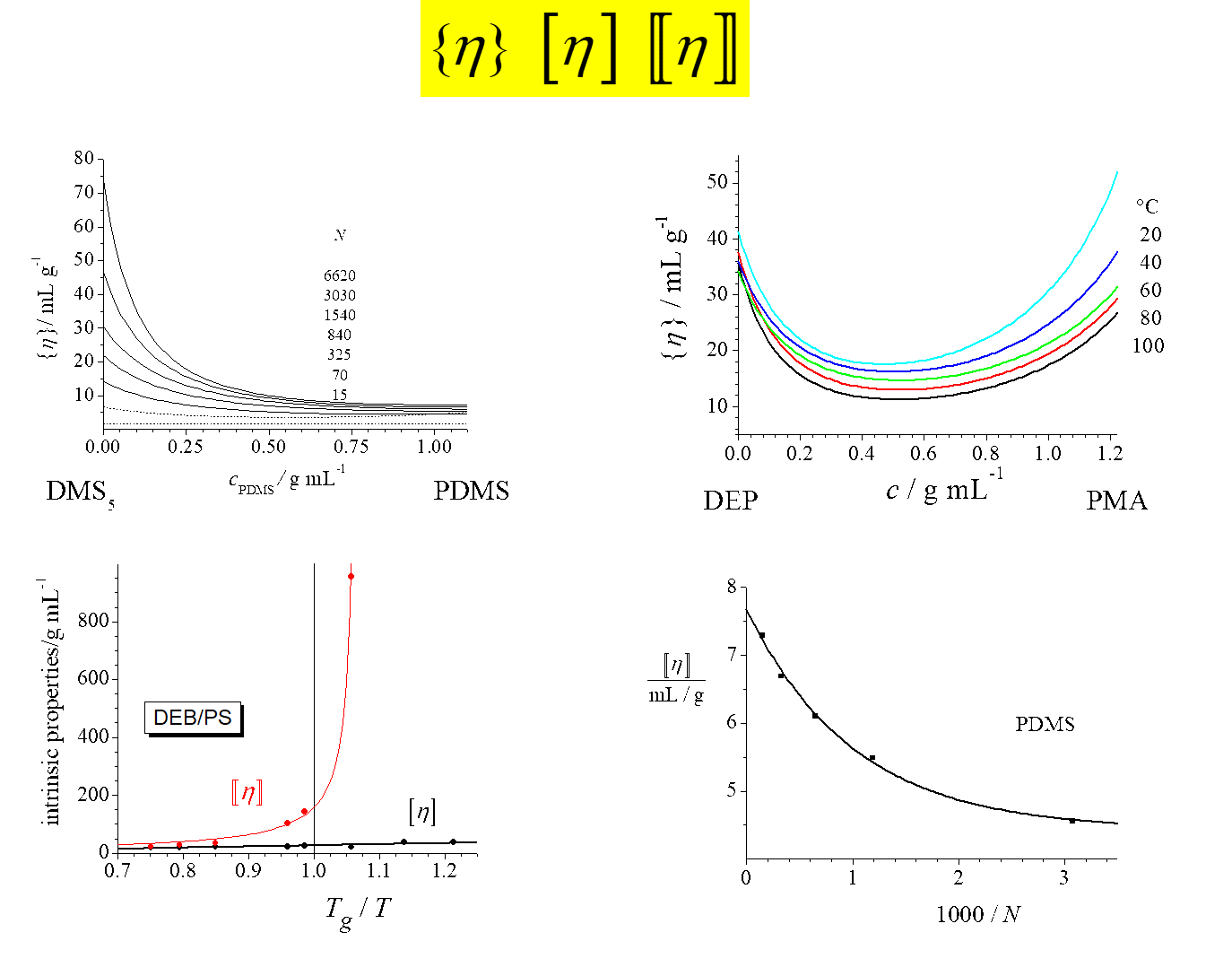
Looking at the graphs clockwise: The first diagram shows the behavior for solutions of poly(dimethylsiloxane) in its pentamer for different degrees of polymerization; the next diagram refers to solutions of poly(methyl acrylate) in diethyl phthalate at different temperatures. The third one demonstrates that \([\kern-0.15em[ \eta ]\kern-0.15em]\) approaches a finite limiting value for infinitely long chains, in contrast to \(\left[ \eta \right]\), and the last diagram compares the temperature dependence of \(\left[ \eta \right]\) and of \([\kern-0.15em[ \eta ]\kern-0.15em]\) for the system diethyl benzene/polystyrene, where \({T_g}\) stands for the glass transition temperature of the pure polymer.

The phenomenological expression for the concentration dependence of \(\eta\) over the full range of composition also provide non-calorimetric experimental access to the conditions of glass transition, as detailed below.

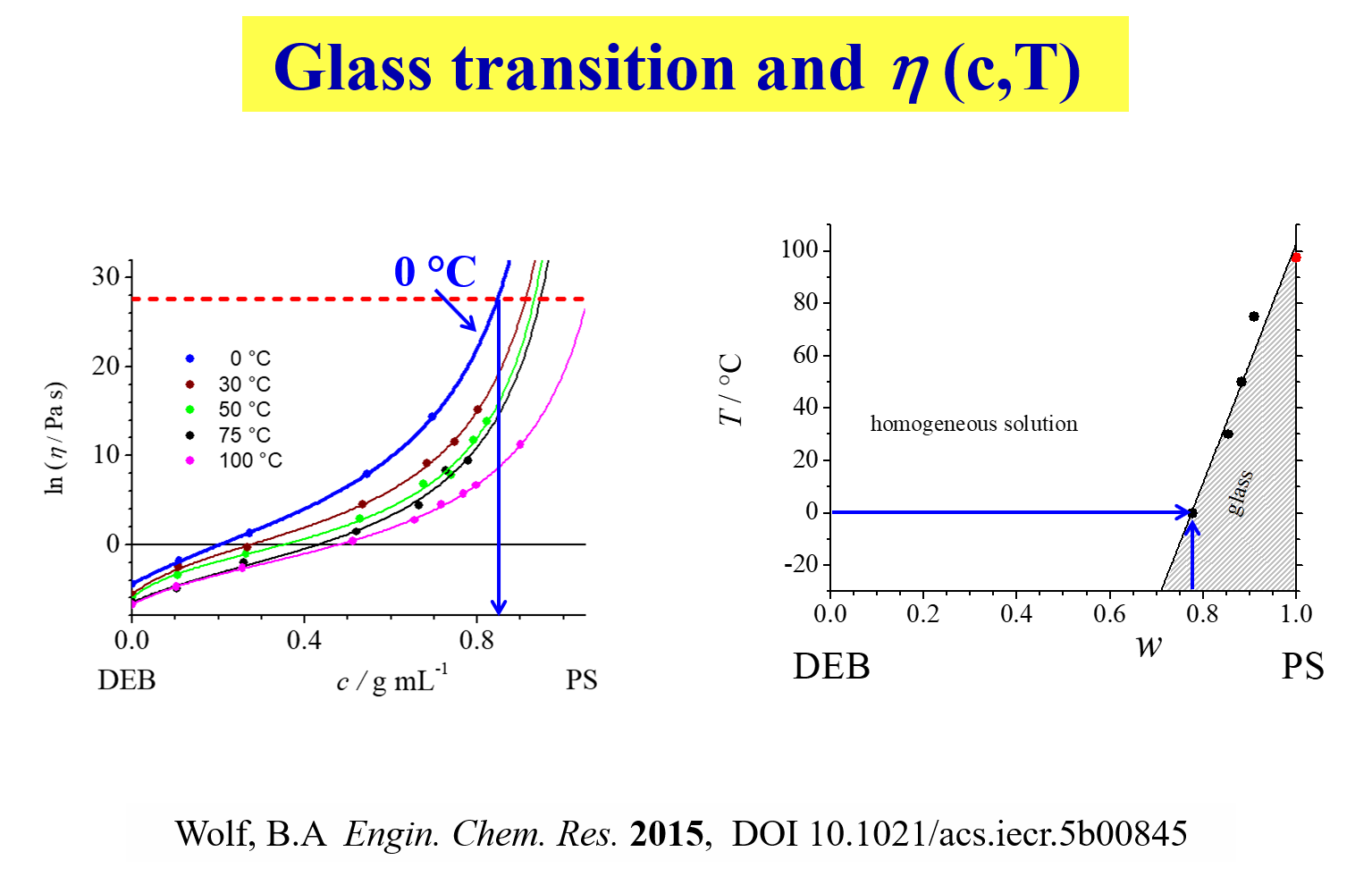
Based on the observation that the viscosity at the glass transition is normally known and more or less independent of the particular system, it is possible to determine the conditions at which the system solidifies at a given temperature [^326]. It is also interesting to note that entanglement molecular weights can be estimated from the sole information on the Newtonian flow behavior[^337] and that the study of molecular weight dependencies yields information on the importance of endgroups for the flow behavior.

Another finding which deserves explicit mentioning concerns a molecular model for the description of the viscosity of polymer/solvent systems[^207] [^220]. It is based on three premises: (i) the dissipation of energy takes place at the molecular interfaces; (ii) the friction between solvent and solute varies with composition due to a change in the flow mechanism (drainage of coils); and (iii) the specific coil volume generally also depends on polymer concentration. The resulting simple expression contains four system-specific parameters: a geometric factor \(\gamma\), which accounts for the differences of the surface to volume ratios of the components; a viscometric interaction parameter \(\alpha\), which measures the friction between solute and solvent in the case of fully draining polymer coils; \(\left[ \eta \right]\) , the specific hydrodynamic volume of the polymer at infinite dilution (intrinsic viscosity), and \({\left[ {\eta } \right]_\Theta }\) the specific hydrodynamic volume under theta conditions. The suitability of this model is demonstrated by means of extensive experimental data reported in the literature for the systems diethyl phthalate/poly(vinyl acetate) and diethyl phthalate/poly(methyl acrylate).

The relationships for the composition dependence of \(\eta\) discussed so far, turn out to be particularly helpful for the modeling of viscometric behavior of polyelectrolytes in dilute solution as detailed in the next section.

Polyelectrolytes

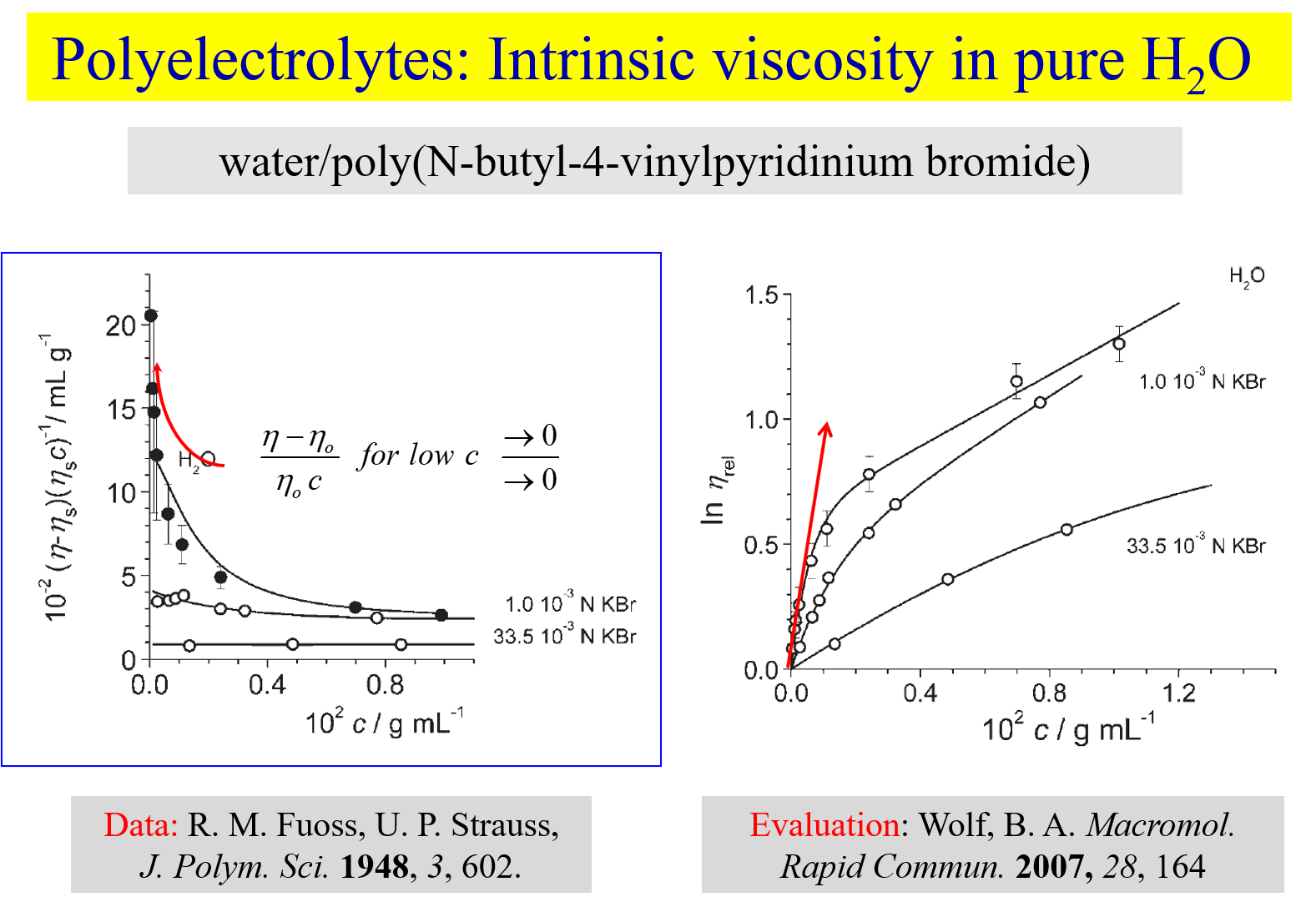
The linear extrapolation of \((\eta - {\eta _o})/({\eta _o}c)\) towards \(c \to 0\) constitutes the basis of traditional methods to determine intrinsic viscosities \(\left[ \eta \right]\), where \(\eta\) is the viscosity of polymer solutions of concentration c and \({\eta _0}\) is the viscosity of the pure solvent (cf. left hand side of the above chart). With uncharged macromolecules this procedure works well; for polyelectrolytes it fails because of the pronounced non-linearity of the above dependence at high dilution resulting from the increasing electrostatic interactions. The alternative definition of the intrinsic viscosity presented in the first part of this chapter does not suffer from this deficiency[^280] [^286], as shown on the right hand side. It is therefore for instance suited for the study of salt influences. The two graphs of the next chart give an example referring to the system water/sodium polystyrene sulfonate[^286].

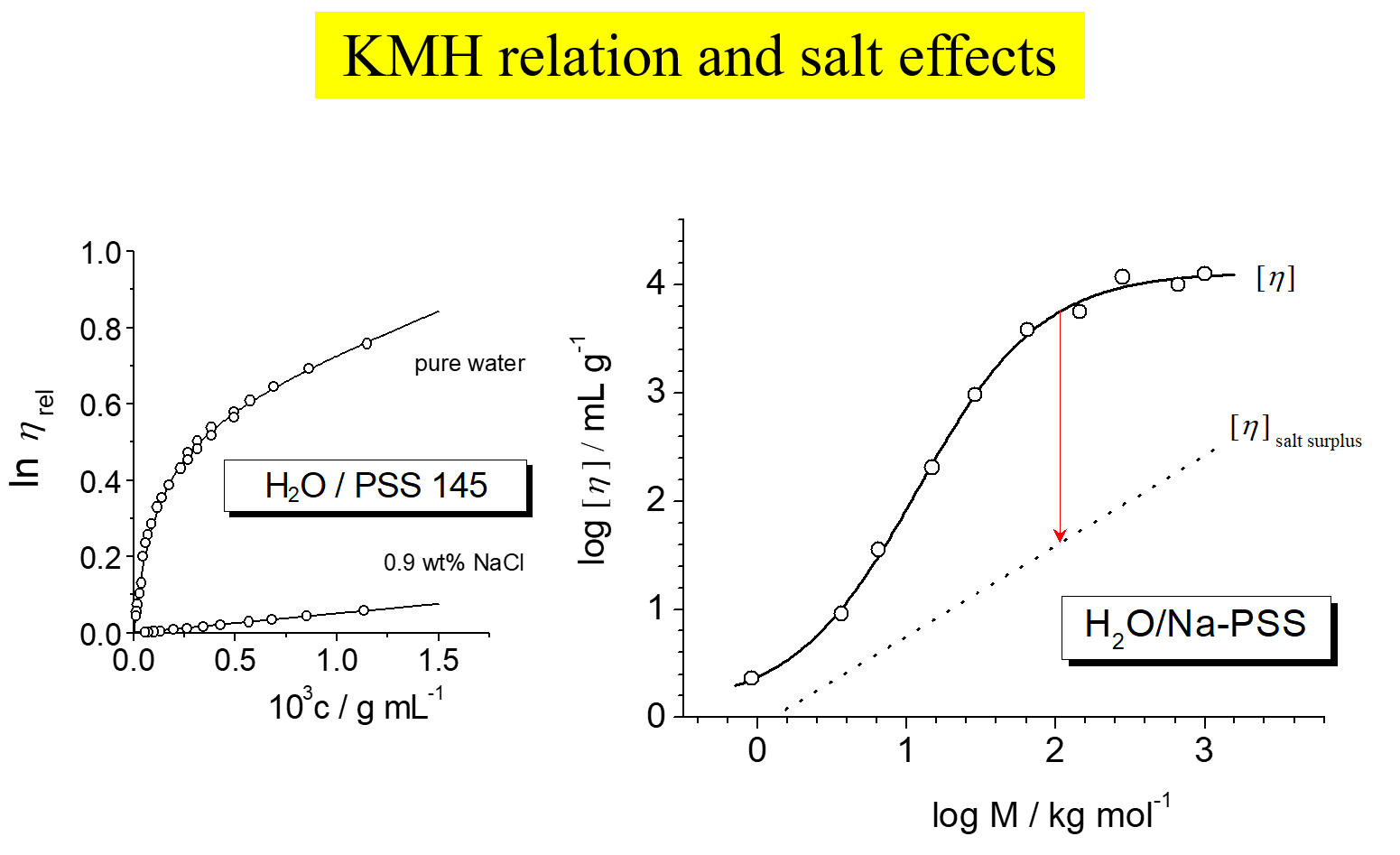
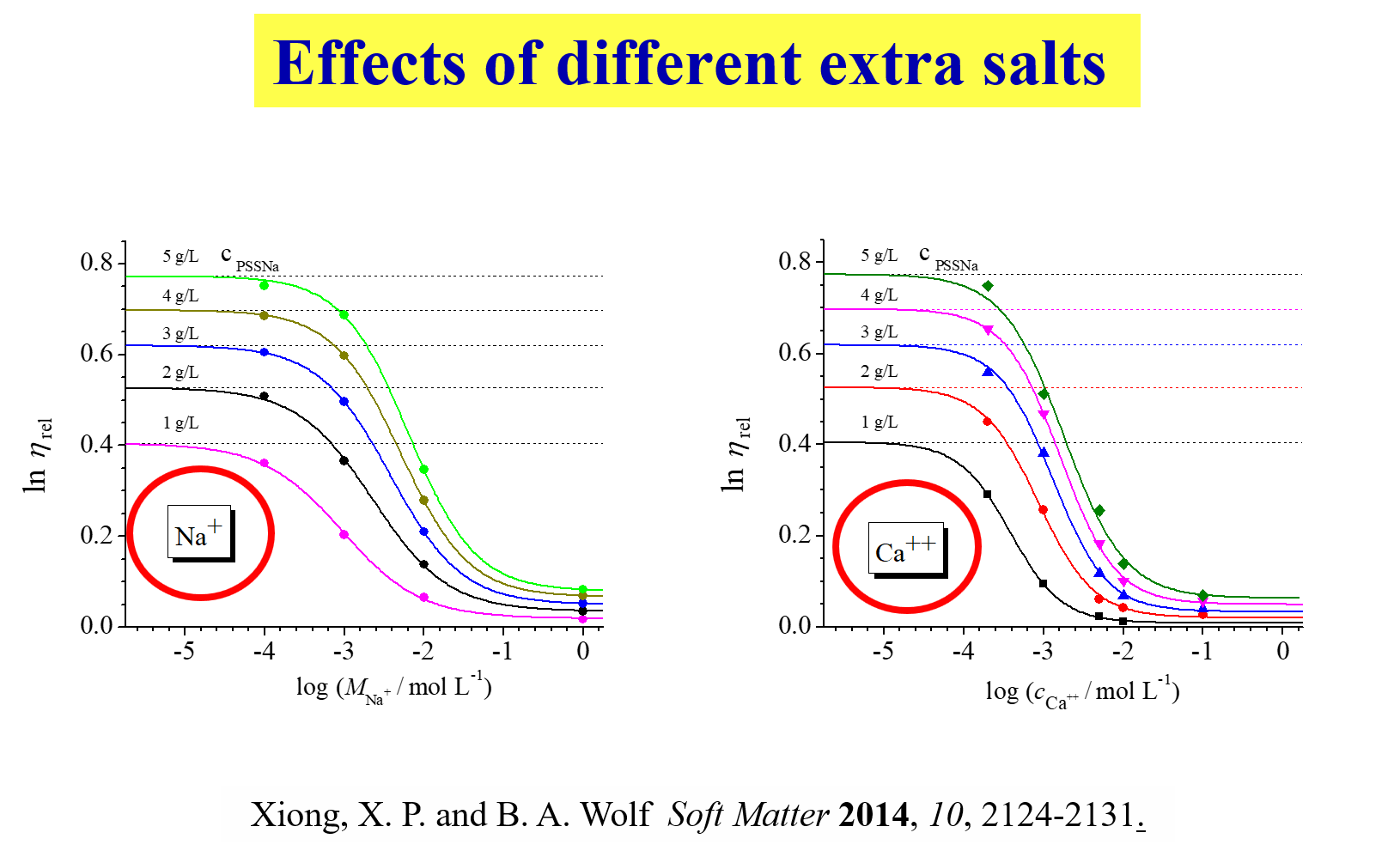
The first diagram shows the evaluation of the primary data; the intrinsic viscosities obtained from the initial slopes of such curves yield intrinsic viscosities and the Kuhn-Mark-Houwink relation shown on the right. The chain expansion resulting from the repulsion of the charges attached to the polymer backbone in pure water leads to intrinsic viscosities, which are up to two orders of magnitude larger than at high salt concentrations in the solvent. Investigations, analogous to those shown for sodium polystyrene sulfonate, were also performed for carboxymethyl guar[^291], branched polyelectrolytes [^292], ionic polymers based on dextran[^295] and with complex systems like BSA plus dextran[^323]. We have also compared the behavior of star-like and linear polyelectrolytes[^332] and self-shielding with salt-shielding[^328]. The effects of chemically dissimilar ions [^320] on the flow behavior appear particularly interesting in view of the expectable importance of biological processes, as demonstrated below.

A further phenomenon, which is strongly related to polyelectrolytes – but not restricted to them - concerns the self-organization of different kinds of macromolecules. The creation of polyelectrolyte complexes is one example[^316] the formation of complexes between charged and uncharged macromolecules[^335] is another. The observation that mixed isolated coils can under certain conditions be formed in sufficiently dilute joint solutions of polymer blends represents an unexpected finding[^334]. It is probably the simplest example for self-organization and constitutes a strong indication for very favorable interactions between the dissimilar polymer segments, i.e. for polymer compatibility.