Interrelation of thermodynamic and flow effects

Phase separation as a function of shear

The first report on a change in the phase behavior of polymer solutions caused by its flowing, dates back to 1950 (Silberberg, A.; Kuhn, W. Nature 1950, 170, 450); these authors observed an extension of the homogeneous region by shear, a phenomenon we subsequently for short call SIM (shear induced mixing). Since then numerous further studies have dealt with the influences of shear on the conditions of phase separation. They testify rather complex relationships, like SID (shear induced demixing) in addition to SIM and the creation of islands of immiscibility as will be discussed below.

The magnitude of the effects depends strongly on the nature of the system. For mixtures of low molecular weight compounds the consequences are minute and hard to measure. In the case of polymer solutions, the changes in the demixing temperatures are typically on the order of a few degrees. The largest effects are observed for polymer blends and for their solutions in a common solvent, where they can reach up to 100 °C.

The methods applied for studies of the present type are manyfold. We came across the phenomena first in the course of experiments on the pressure influence on the viscosity \(\eta\) as shown in the following chart[^041].

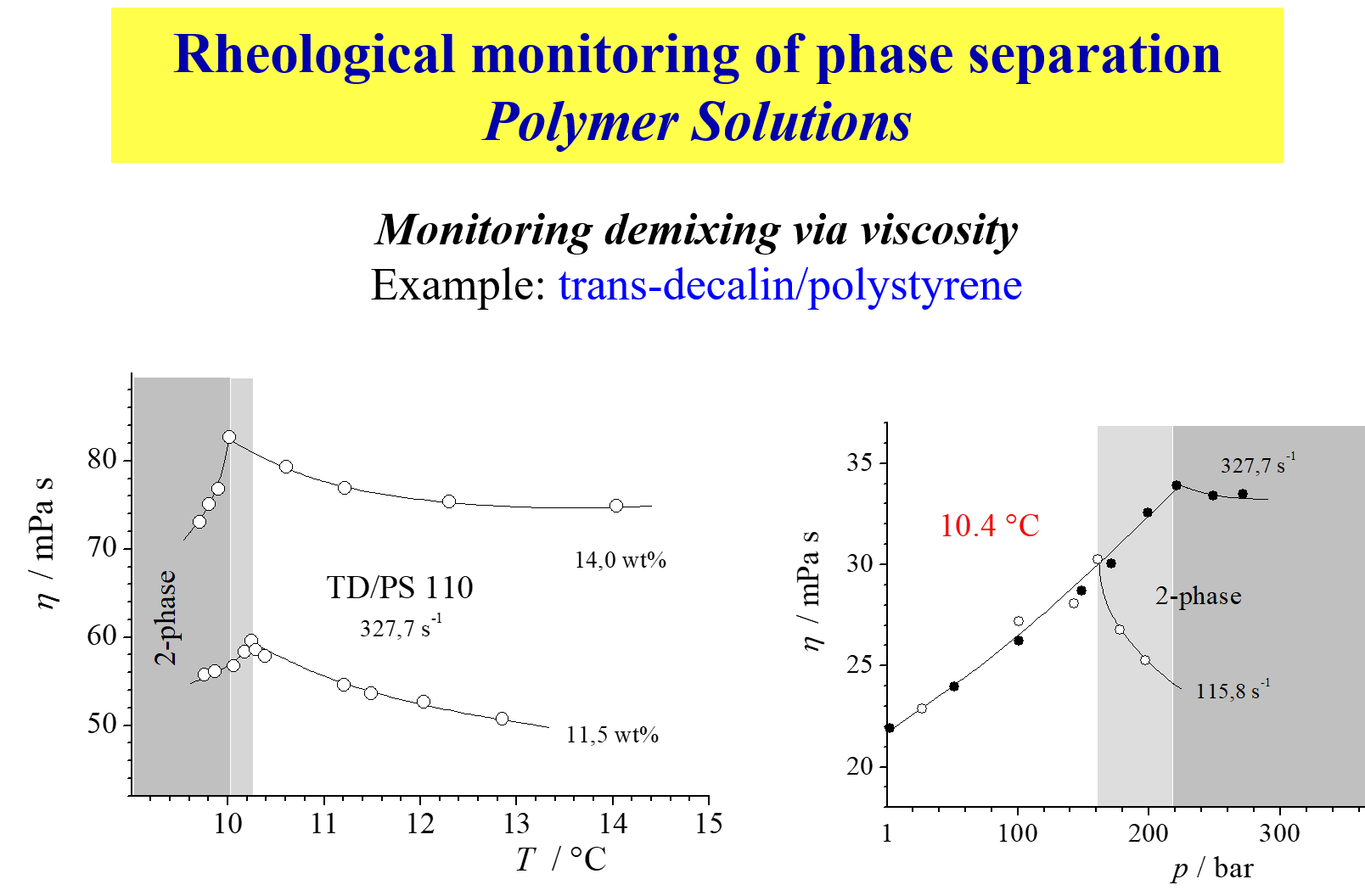
The system trans decalin/polystyrene exhibits SIM; the left graph gives the result for atmospheric pressure as a function of T and the right graph shows the pressure dependence at constant temperature for different shear rate (\(\dot \gamma\)).

Shear influences on phase separation can also be determined by rheo-optical methods. The apparatus[^081] we used for that purpose is shown next.

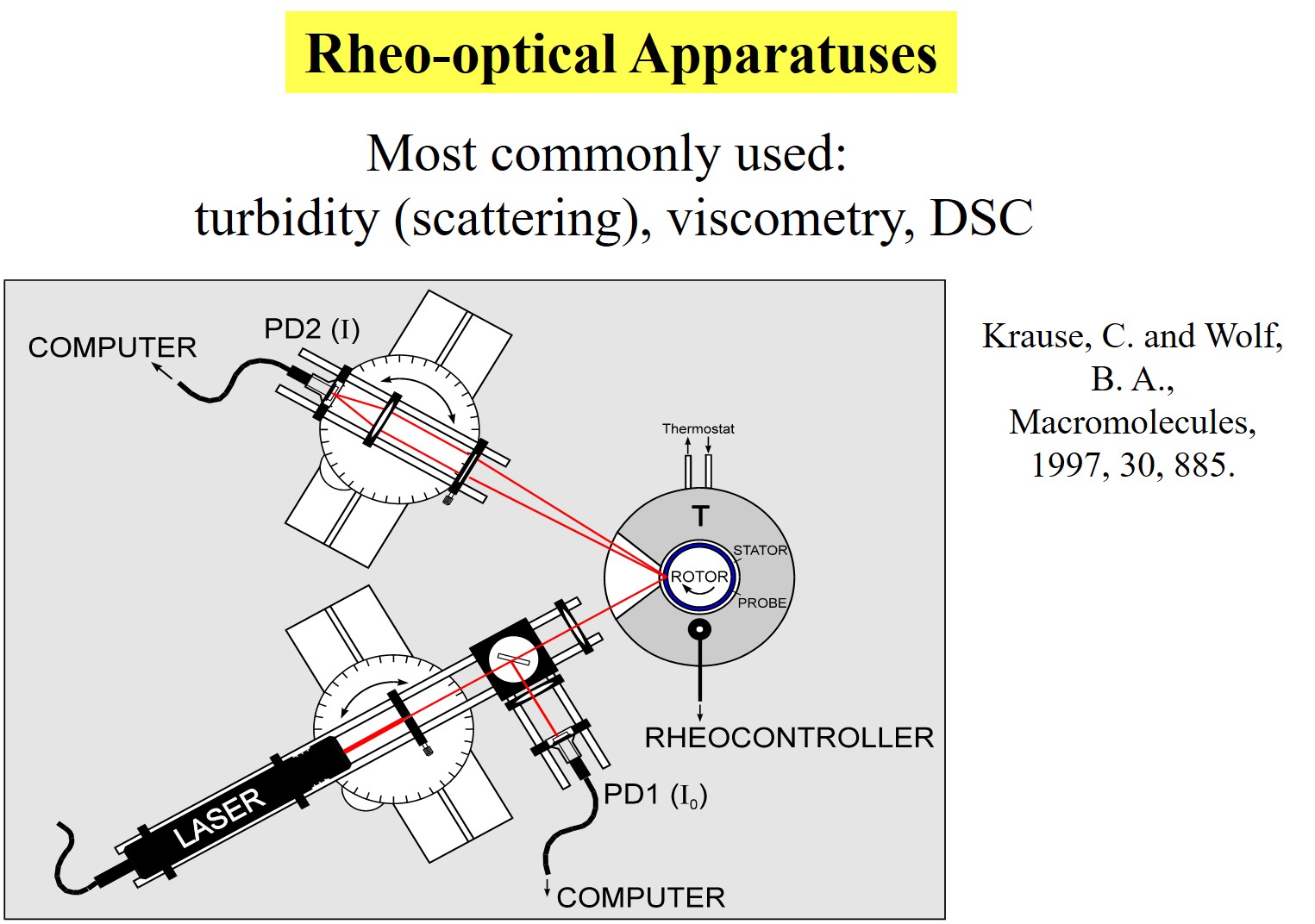
In the course of our studies we have observed a multitude of phenomena. The following charts give some examples; for more information please search the section "Publications".

In case of ternary systems the shear effects may become particularly pronounces as far as the changes in the demixing temperatures are concerned[^173], as demonstrated by means of the next chart

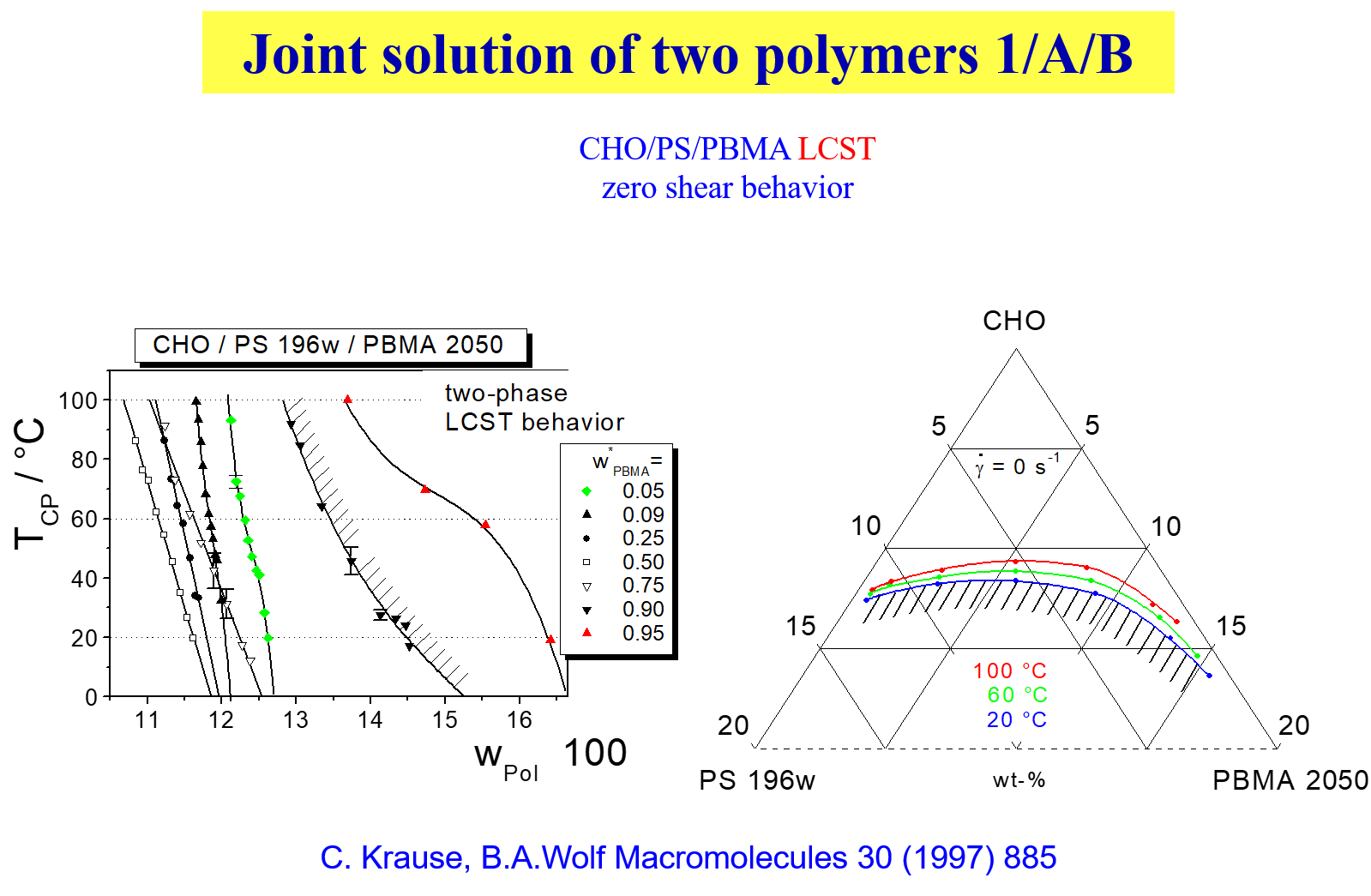
With certain polymer solutions (e.g. polystyrene in trans decalin) on the other hand one observes[^081] a change from SIM to SID as the molecular weight of the polymer rises. Furthermore it is interesting to note that even blends of oligomers depend in their phase behavior on shear[^142].

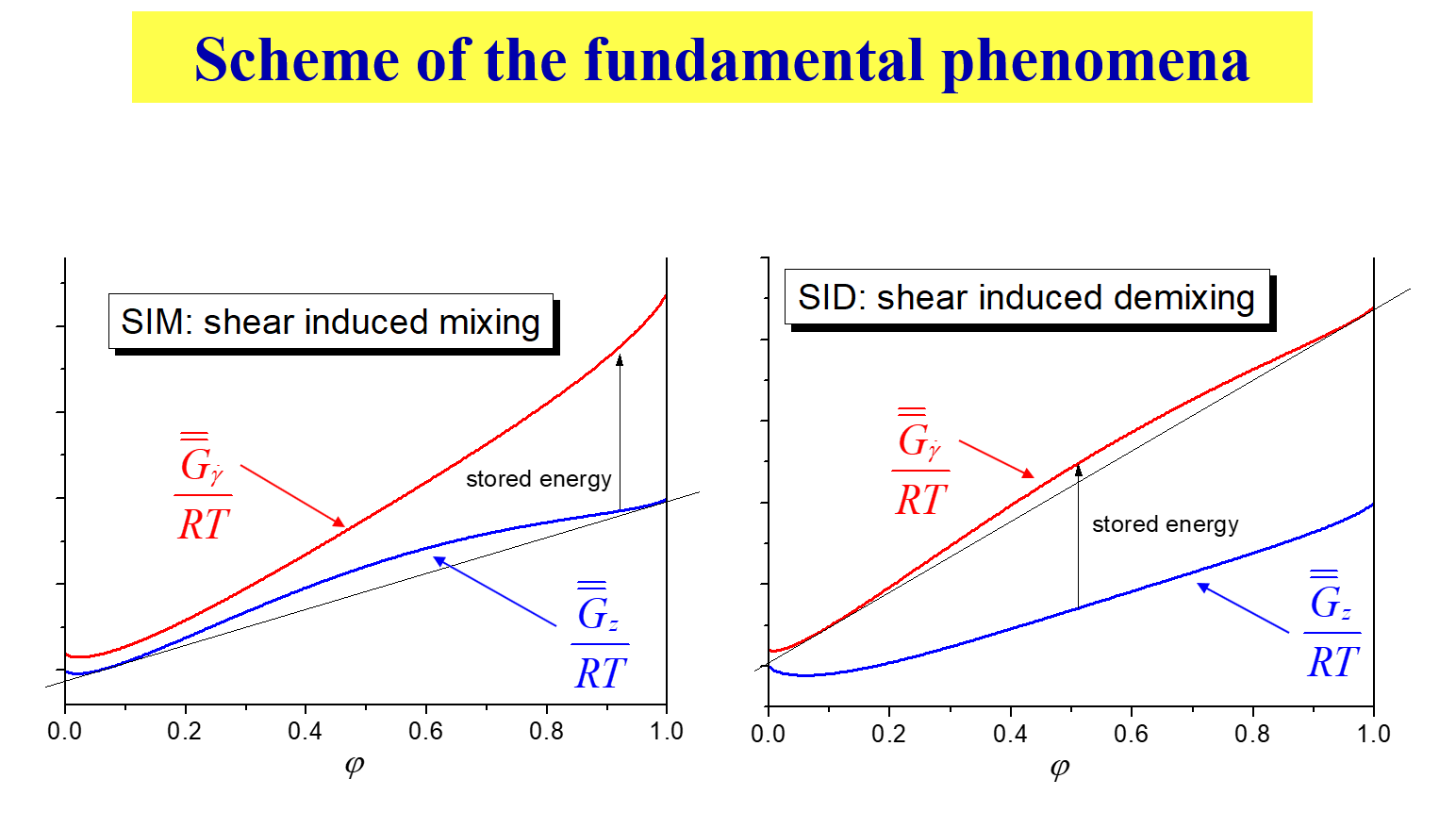
In order to rationalize the multitude of phenomena observed, we have introduced the generalized Gibbs energy of mixing, \({G_{\dot \gamma }}\), accounting for the fact that the systems are no longer at rest. The next two charts depict the central idea of that approach[^068].

\({\overline{\overline G} _{\dot \gamma }}/RT\), the base molar, reduced Gibbs energy of mixing for a given shear rate \(\dot \gamma\), as a function of the volume fraction of the polymer represents the central quantity for the calculation of phase separation. The following scheme demonstrates how the behavior of stagnant mixtures (blue lines) changes upon the addition of the stored energy. The example shown on the left eliminates the hump prevailing at rest, i.e. depicts SIM. The opposite, the production of such a hump (SID), is depicted on the right.

The next chart displays an example for theoretical calculation rationalizing experimental observations[^108] [^189] for polymer solutions; TD = trans decalin, PS = polystyrene

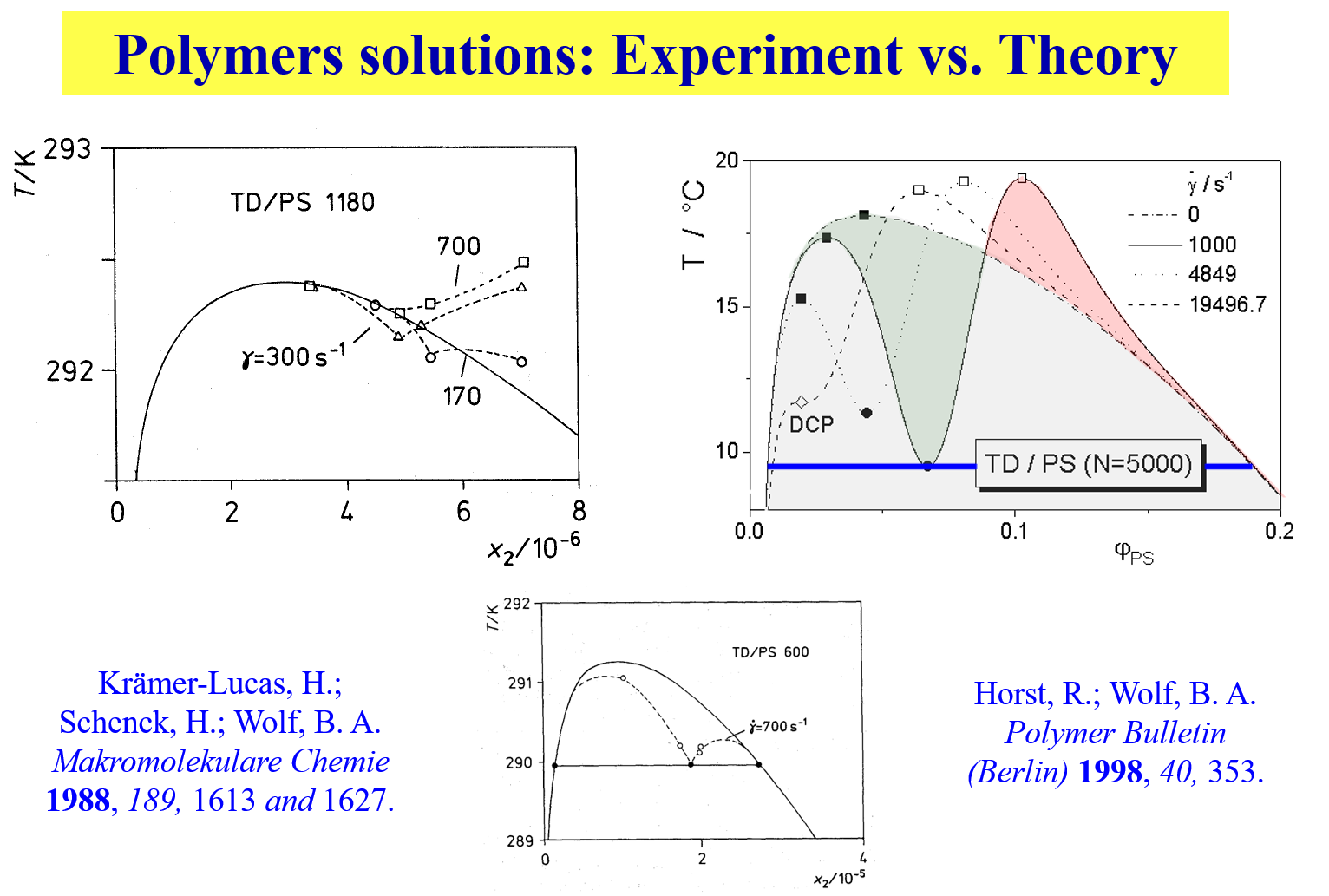
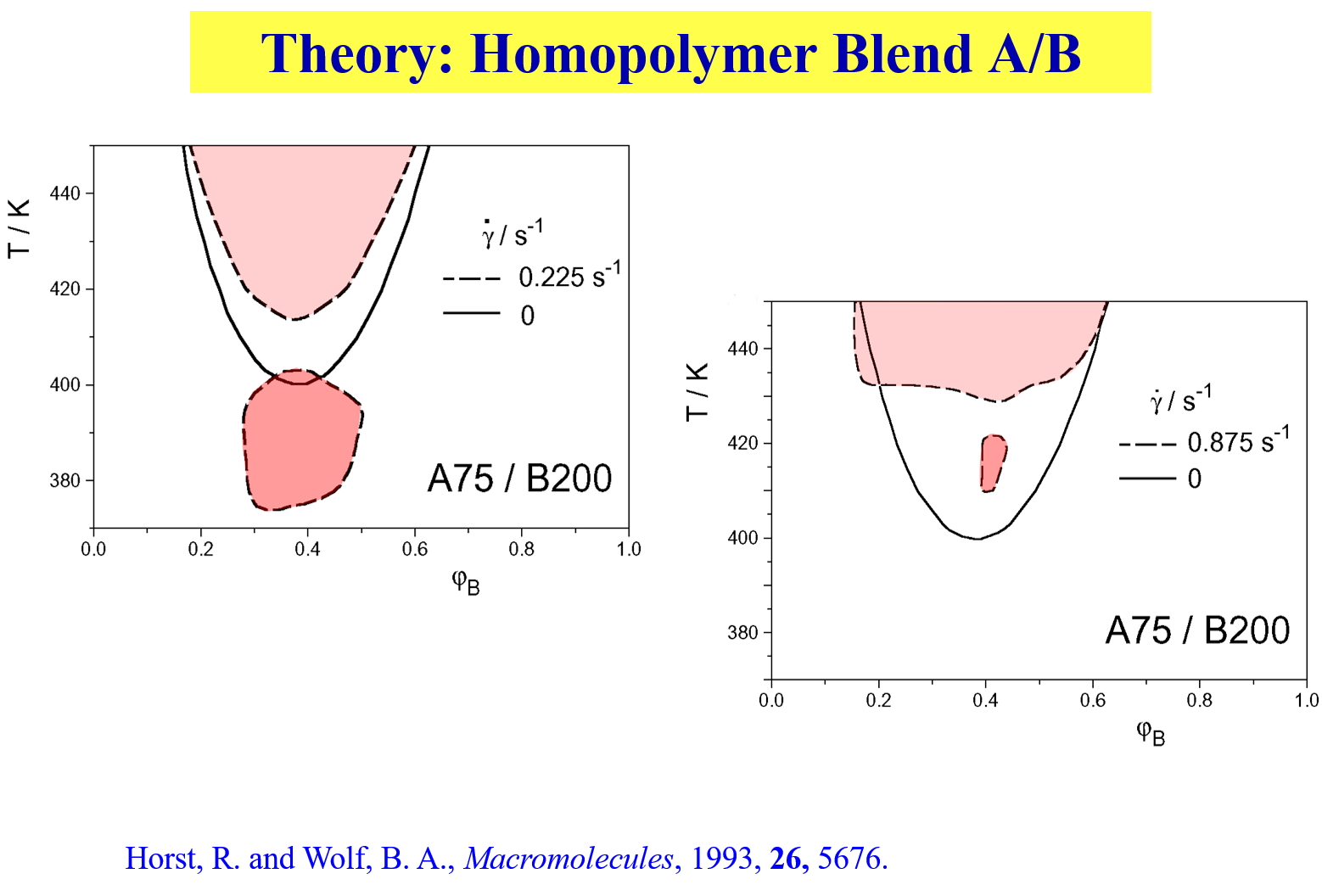
Polymer blends may exhibit special phenomena as shown below[^137]. Depending on the particular shear rate, outer or inner islands of immiscibility are created.

Thermodynamic influences on the flow behavior

So far we have discussed the influences of shear on phase separation. The thermodynamic influences on the flow behavior of polymer containing fluids are not yet studied as systematically as the shear influences on demixing. For the qualitative understanding it is important to distinguish between the effects prevailing in the dilute range (individual coils dominate) and the effects prevailing at high concentrations (fully developed entanglement network). In the former case a reduction in solvent power leads to coil shrinkage and as a consequence to a diminution of the viscosity \(\eta\). The effect is opposite in the latter case because of the thermodynamically preferred intersegmental contacts. Under such conditions the monomeric units tend to stay together, even as the system flows. This phenomenon, which we have called "pull-along effect"[^053] leads to an increase in \(\eta\) upon a decrease in solvent power.

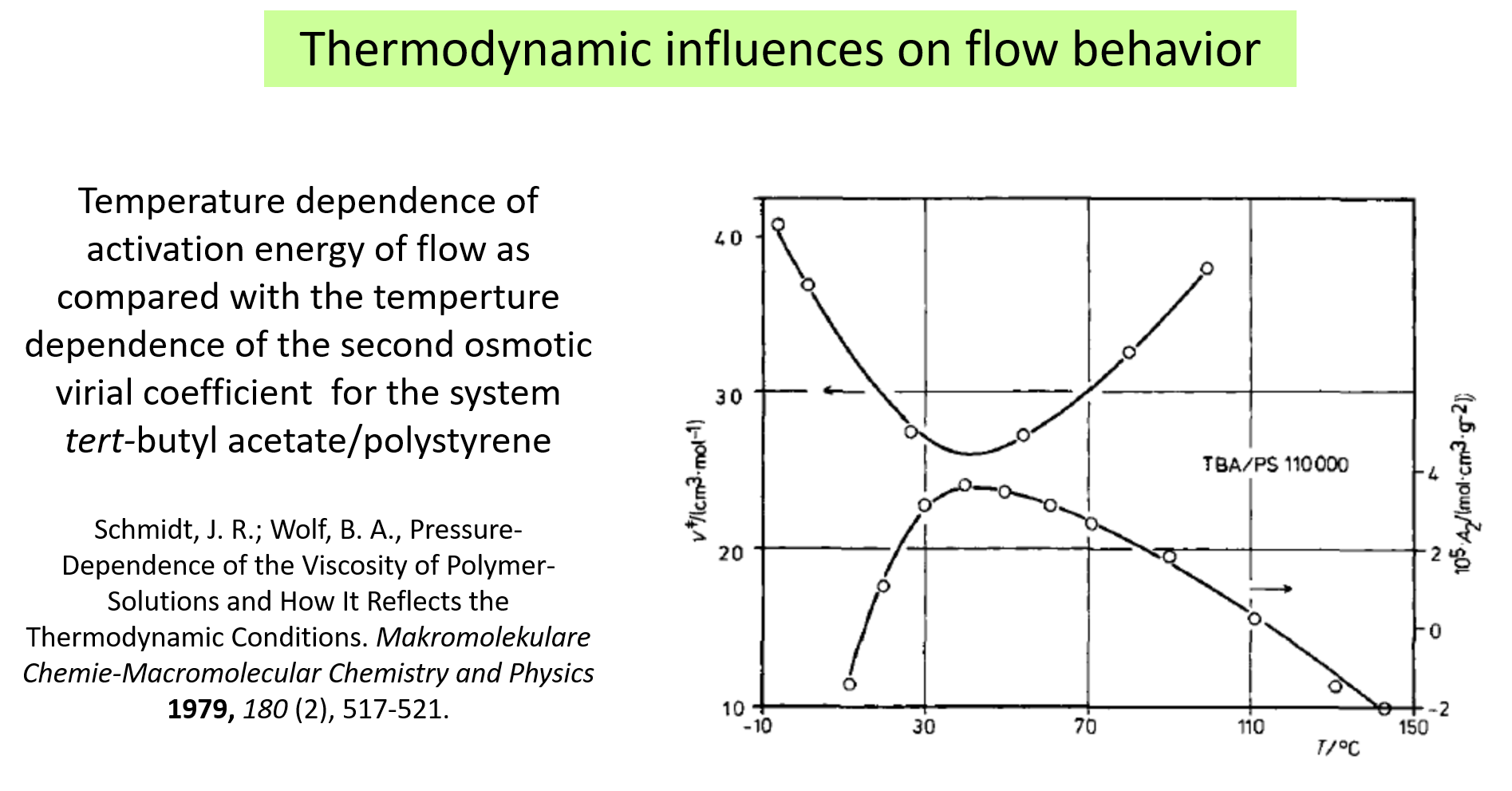
The following charts show some examples for the thermodynamic influences on the flow behavior. The next illustrates how the pressure dependence of \(\eta\) (as quantified by the activation volume of flow) correlates with the solvent quality (expressed in terms of the second osmotic virial coefficient) [^042].

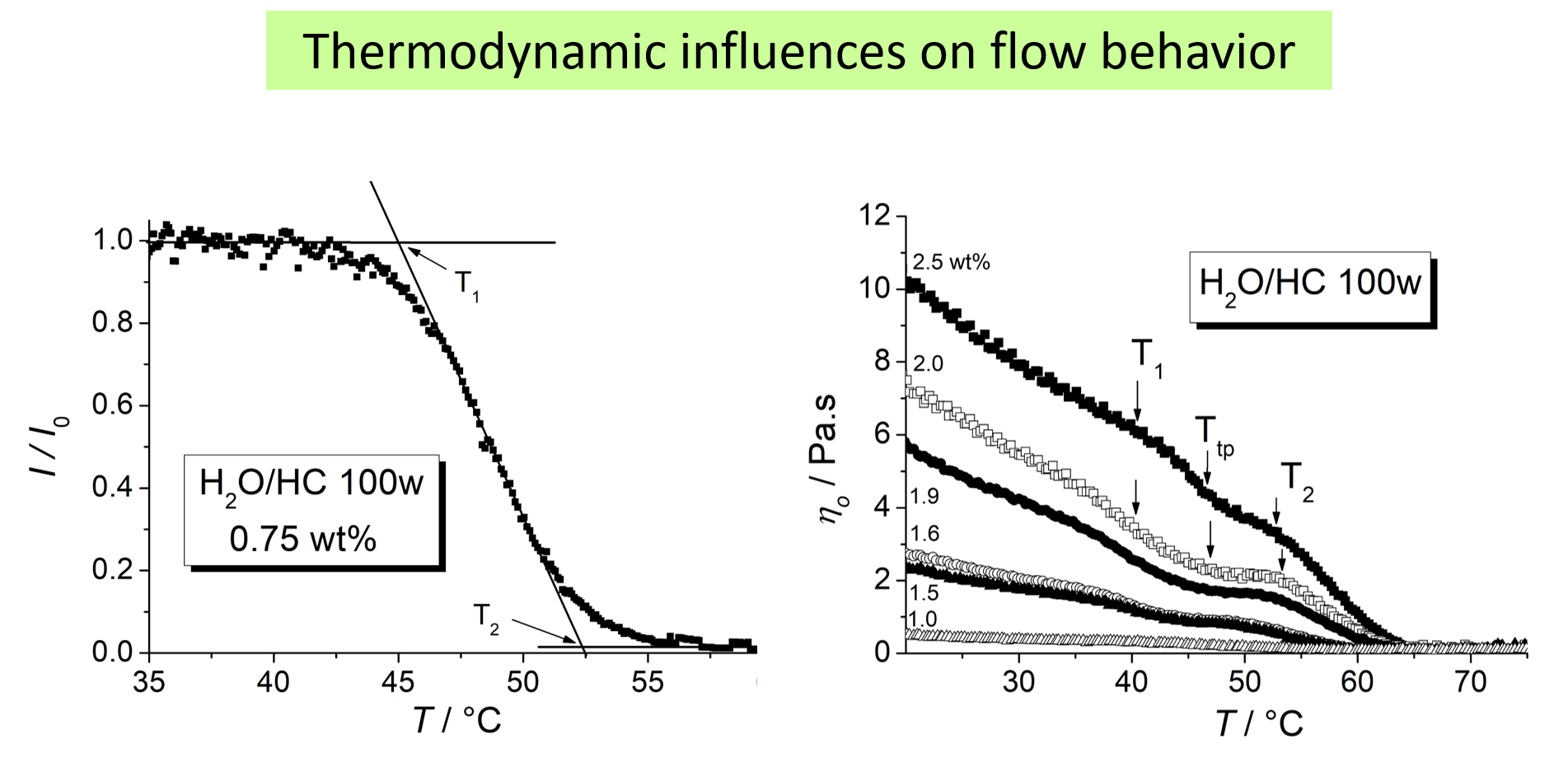
Another example for which the effects can be seen more directly refers to aqueous solutions of hydrophobically modified ethyl hydroxyethyl cellulose exhibiting LCST behavior[^200]. The left part of the chart displays how the light transmittance goes down upon heating. The reaction of the viscosity on these thermodynamic changes is displayed on the right hand side.

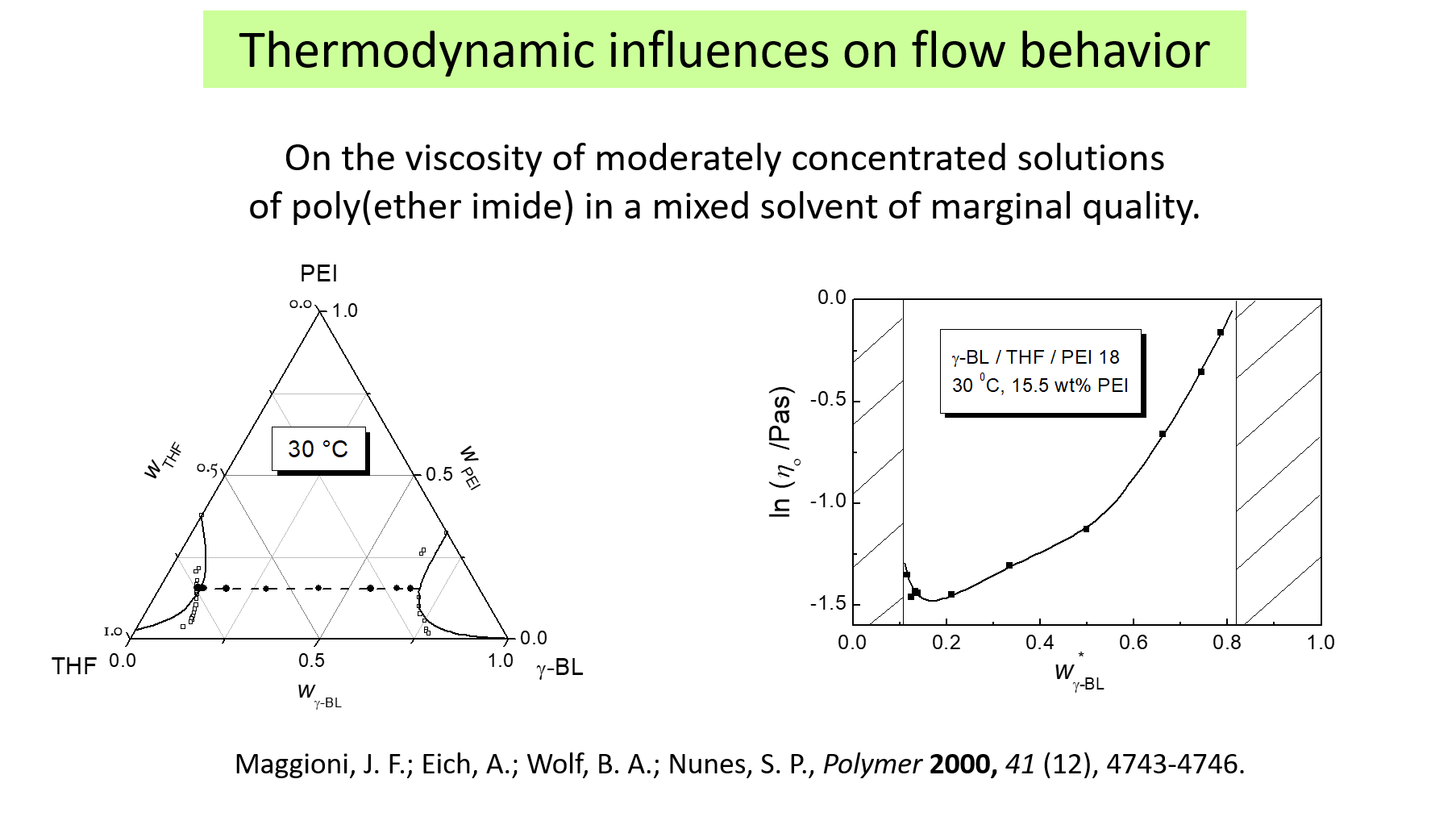
The interrelation of viscometric and thermodynamic effect becomes particularly pronounced in the case of polymer solutions in mixed solvents. The following example concerns solutions of poly ether imide in tetrahydrofurane plus \(\gamma\)-butyrolactone. This system displays the phenomenon of cosolvency, which means that the individual solvent components exhibit a miscibility gap with the polymer, whereas some of their mixtures are good solvents, as depicted in the phase diagram shown on the left. In the light of the pull-along effect, discussed above, it obvious that the dependence of the viscosity on the composition of the mixed solvent shown on the right hand side displays the solvent quality. According the these results it is highest at about 15 wt% of \(\gamma\)-butyrolactone.

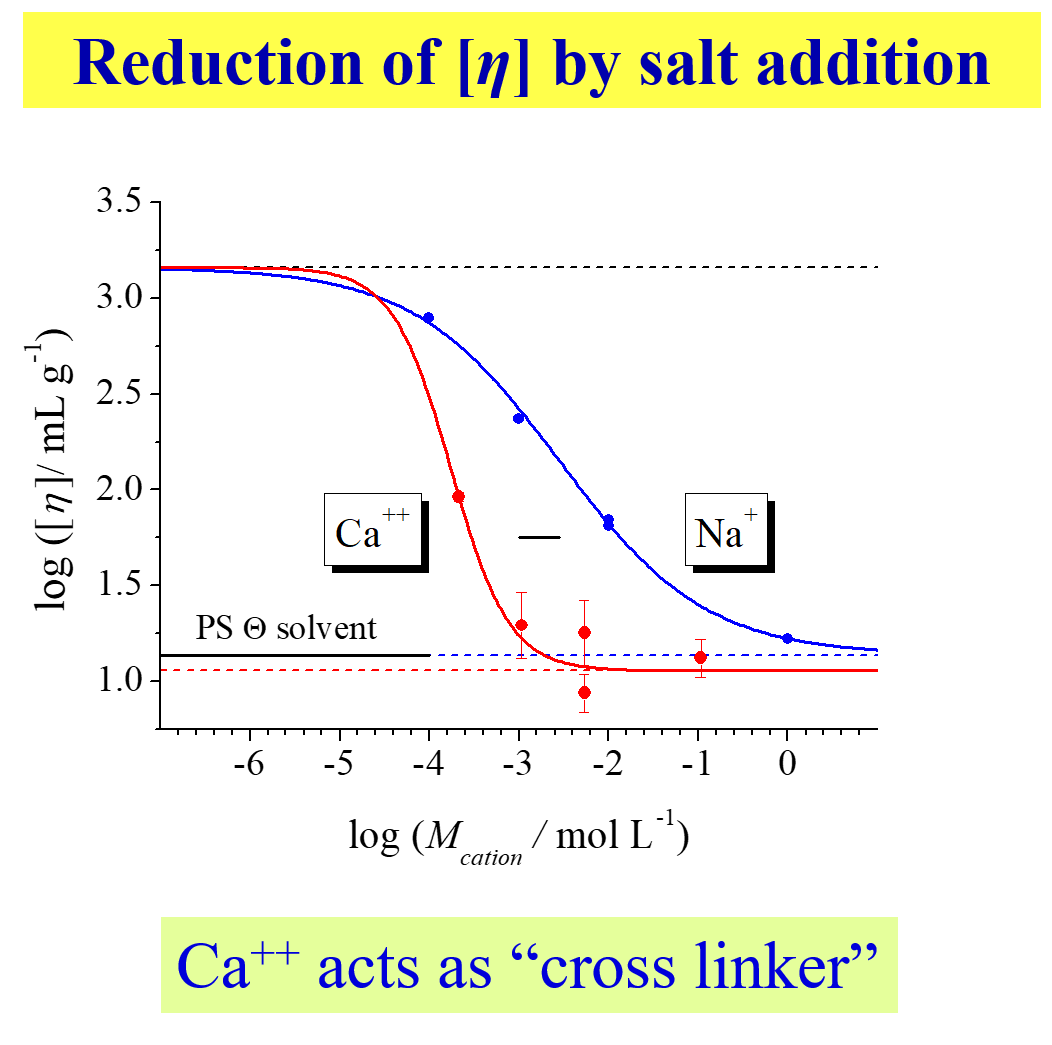
The last two instances demonstrate how general the interrelations of the present type are. The following[^320] describes the variation of the intrinsic viscosity for the salts of polystyrene sulfonic acid in water with the molarity of the cation. The earlier and much steeper reduction of the intrinsic viscosity for \(C{a^{ + + }}\) as compared with \(N{a^ + }\) is a consequence of the more favorable interaction of the former cation with the \(SO_3^ -\) groups and of its crosslinking ability.

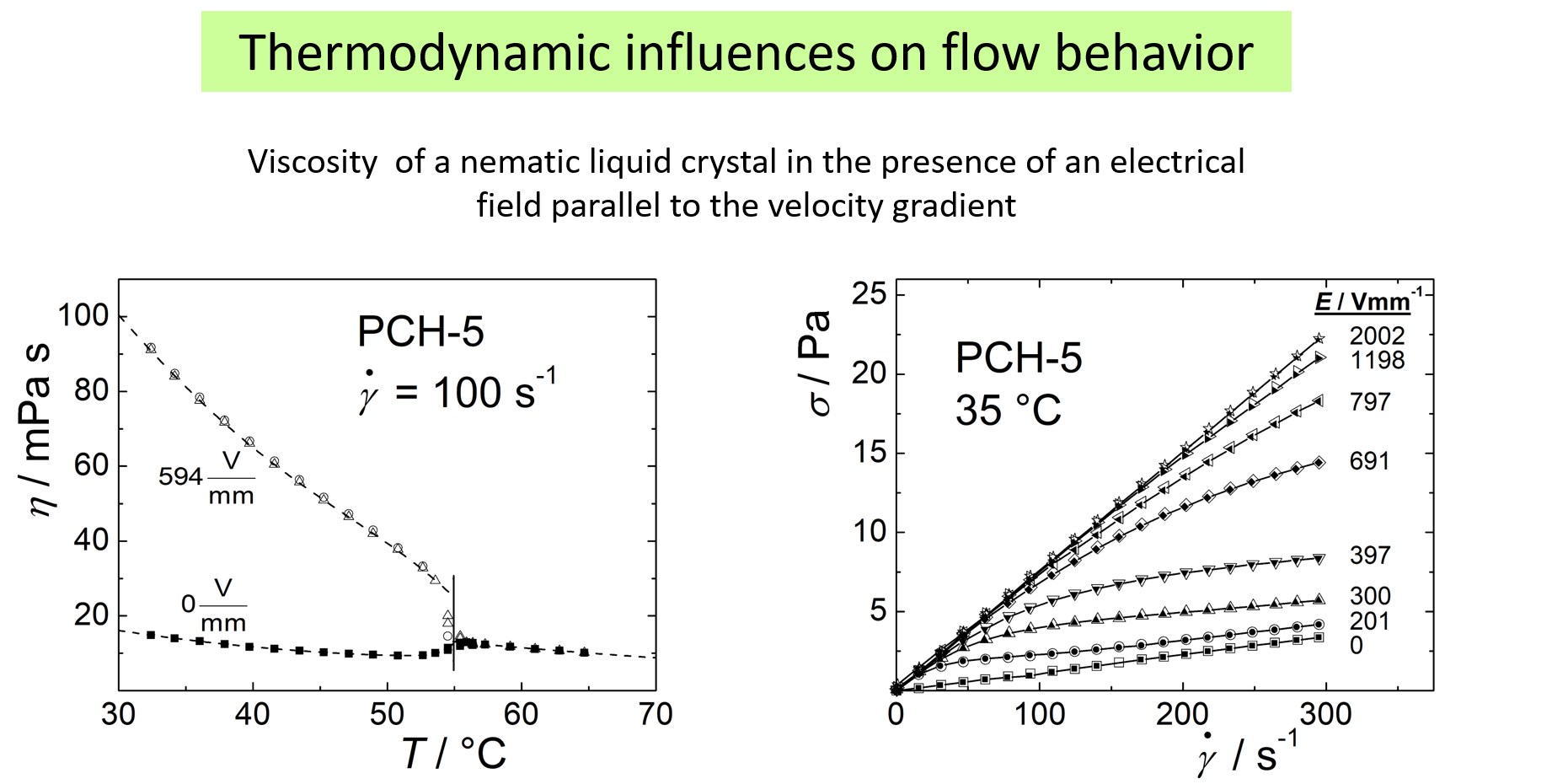
The next example[^211], referring to the low molecular weight liquid crystals, 4-(trans-4'-pentylcyclohexyl)-benzonitrile, shows that thermodynamic effects on the flow behavior are not restricted to polymers or to mixtures. In this case it is the electric field (parallel to the gradient of the velocity) that modifies the thermodynamic situation and thus the flow behavior. The diagram on the left demonstrates that the electric field may increase the viscosity by a factor of approximately 5. The right side of the chart exhibits more details.

Equilibrium versus shear clusters

In common use the term cluster describes “a group of similar things that are close together”. Here it means that polymer segments or entire macromolecules may stay together under certain conditions. For the interpretation of the behavior of polymer solutions, clusters play an important role, as demonstrated by more than twenty thousand hits in the Web of Science, where this expression is normally used in an indiscriminate, qualitative manner only. However, as demonstrated below, it is mandatory to clearly distinguish between equilibrium clusters and shear clusters established under Newtonian flow[^340].

The clustering of segments under equilibrium conditions results from the fact that the monomeric units of a polymer molecule are connected by chemical bonds and that the segments arrange in a manner to minimize the Gibbs energy of mixing in solution. In the case of stationary shear, the minimization of entropy production of the system replaces the equilibrium condition.

The following discussion is based on \(\Omega\), the degree of overlap, because of it is more illustrative than \({c_{{\rm{ cluster}}}}\), the polymer concentration within a cluster. The corresponding values for equilibrium and for shear clusters constitute the ratio of the over-all polymer concentration c and the concentration within the particular type of cluster as shown in the next chart. The value of \({c_{{ \rm{equil}}}}\) is given by the characteristics of the polymer molecule in the particular solution and that of \({c_{{ \rm{shear}}}}\) can be easily calculated by means of the generalized intrinsic viscosity (please cf. the section Rheological behavior/concentration influences).

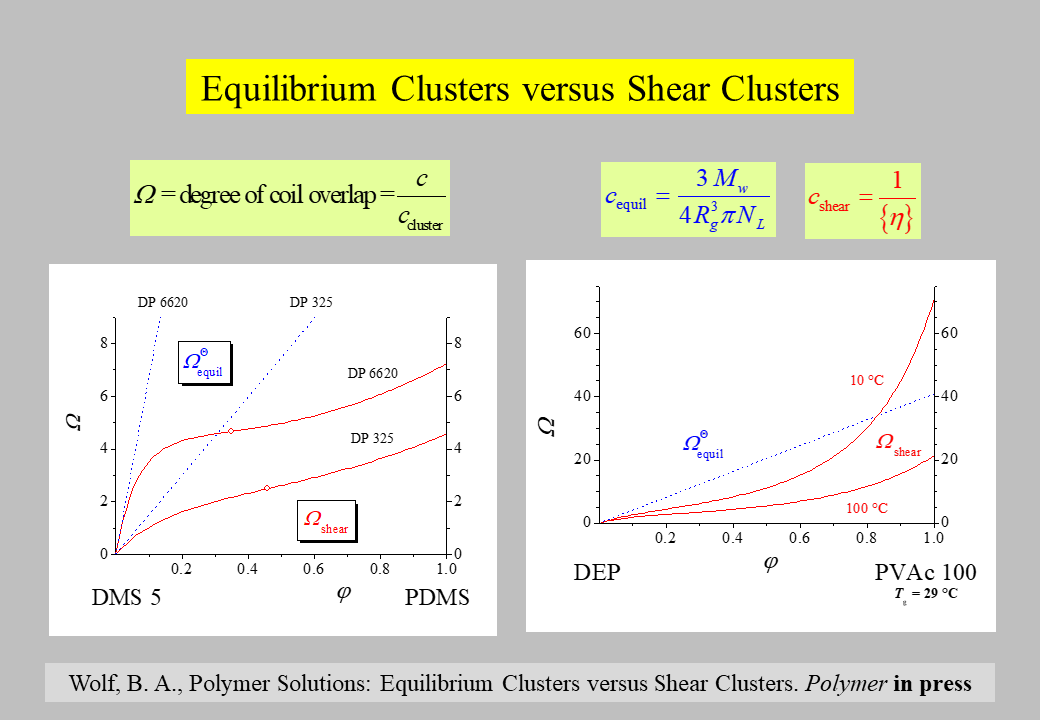
Equilibrium overlap parameters are in almost all cases considerably larger than shear overlap parameters, irrespective of polymer concentration. One exception is that the two parameters become identical in the limit of infinite dilution (isolated polymer coils). The other exception concerns the behavior of systems in the vicinity of the glass transition temperature of the polymer and at high polymer concentrations. Under such conditions the shear overlap parameter may exceed the equilibrium overlap parameter due to particularly favorable interactions between polymer segments belonging to different macromolecules as shown in the right hand side graph.