Solidification and morphology

This section deals with the two viscometric aspects not treated so far. (i) Phenomena that are observed as homogeneous polymer containing systems are cooled to temperatures at which they do no longer flow within reasonable times and (ii) shear influences on two coexisting liquid phases.

Solidification: This part focuses on gelation and its possible correlation with glass transition. The glass transition itself was already subject of discussion in the section "Concentration influences".

Experiments with the system 2-propanol/ poly(n-butyl methacrylate) have shown[^122] that the two phenomena are closely related.

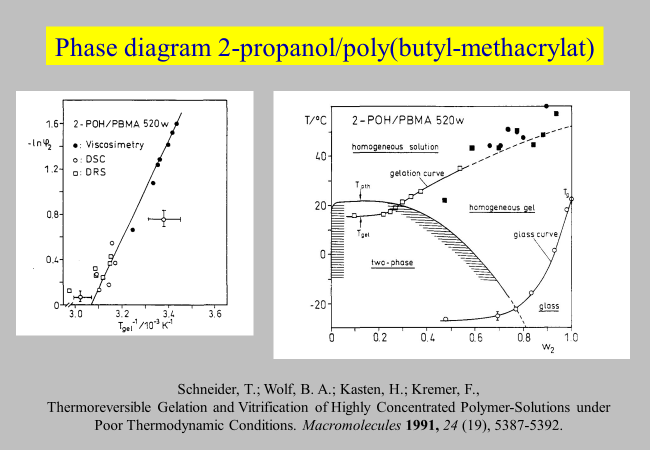
The right-hand side diagram of the above chart demonstrates that the glassy solidification of this system upon cooling starts with the formation of gels at some 60 to 20 °C above the glass transition temperature \({T_g}\).

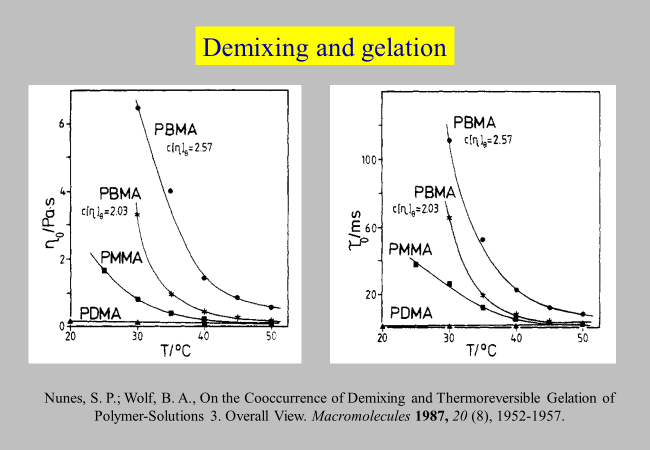
Additional information on the conditions for the gelation of polymer solutions stems from a systematic study[^098] on solutions of poly(n-alkyl methacrylates). These experiments, all performed in theta solvents, have shown (cf. next chart) that the zero shear viscosities and the characteristic relaxation times, \({\tau _{\rm{o}}}\), increase with falling temperature in pronouncedly different manner, despite comparable conditions with respect to the Flory-Huggins interaction parameter. The probable explanation of this observation lies in a proper amphiphilic nature of the monomeric unit in addition to a suitable molecular architecture that enables the formation of enthalpically very favorable interactions via local ordering. Neither too short n-alkyl branches of poly(n-alkyl methacrylates) (like methyl) nor too long ones (like decyl) lead to the cooccurrence of phase separation and gelation, but only a well-balanced length like in the case of the butyl group.

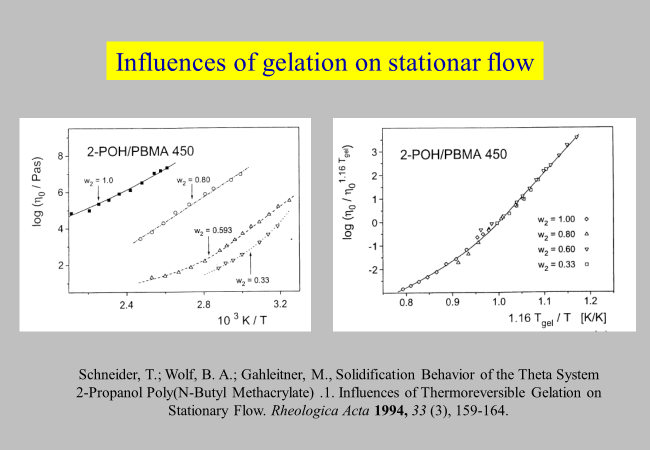
A more detailed study[^149] on the solidification of the theta system 2-propanol/poly (n-butyl methacrylate) has disclosed how thermoreversible gelation manifests itself in stationary flow. The observed temperature dependence of \({\eta _0}\) (cf. next chart) and of the critical entanglement molecular weight, plus the effects of the thermal history on the low temperature viscosities can be rationalized in terms of physical networks formed upon cooling. The increasing average life time and number of intersegmental contacts makes the system "harder", i.e. changes the temperature dependence of \({\eta _0}\) from WLF-like to Arrhenius-like.

An alternative look at solidification phenomena[^220] also deserves mentioning. It replaces the normally used volume fractions as composition variables by surface fractions and demonstrates that the WLF equation describes the increase in \(\eta\) upon a reduction of T below \({T_g}\) only for PBMA adequately, whereas for the isomeric polymers poly(vinyl acetate) [PVAc] and poly(methyl acrylate) [PM(A)] the values are almost four orders of magnitude higher.

2-phase morphology: This section deals with the microscopic structure of sheared two-phase systems. The experimental equipment we have used for that purpose is shown below; the micrograph exhibits a typical matrix-droplet structure.

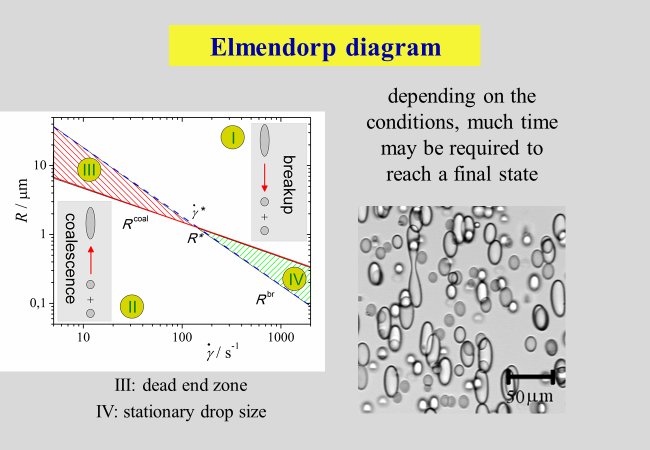
So-called Elemendorp diagrams (Elmendorp, J. J.; Van der Vegt, A. K. Polym. Eng. Sci. 1986, 26, 1332-1338) help to understand, which processes take place for certain combinations of shear rate \(\dot \gamma\) and droplet radii R. Double logarithmic plots of R as a function of \(\dot \gamma\) can be divided into four different zones, as sketched in the next chart. These are: a breakup area (I), a coalescence area (II), a region (IV), within which a stationary drop size is established and finally, a so-called dead-end zone, within which neither coalescence nor bread-up processes are happening (III). For more details please compare reference [^268].

Using a blend of polyethylene oxide/poly(dimethylsiloxane), for which the components have approximately the same viscosity,[^283] we have studied the coalescence processes after an abrupt reduction in shear rate. The next chart shows some results.

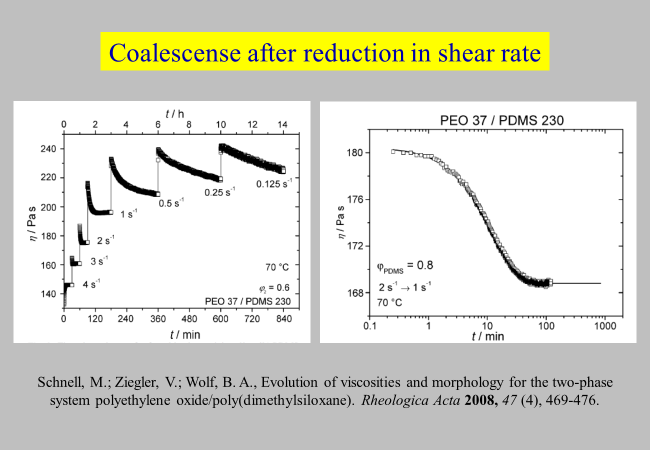
More details are presented in the following chart, in which \({\eta ^\infty }\) designates the viscosity that is attained after infinite time. Also indicated are the viscosities of the blend components and micrographs taken under the specified conditions, where the dark images were received under crossed polarizers and.

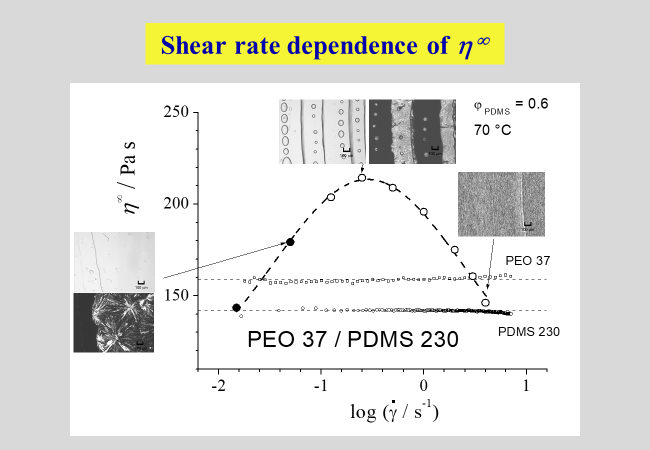
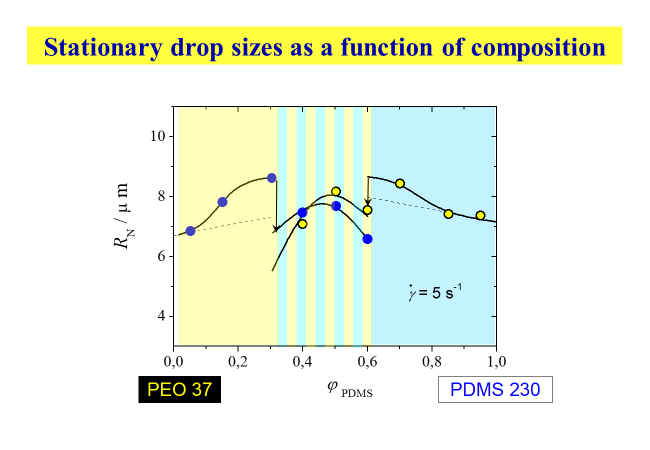
The ranges of different morphology are displayed in the next chart. Within the composition regions close to the pure components, drops of one phase are embedded in the matrix of the other phase; this graph also shows how the radii of the droplets vary with the volume fractions of the components. The range of co-continuity at intermediate compositions (cf. the uppermost micrograph of the last chart) is given prominence by hatching.

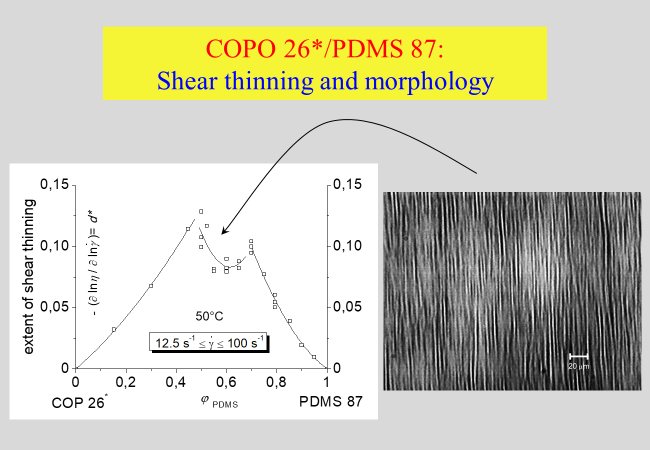
For a blend of chemically very similar, but still incompatible components - (poly(dimethylsiloxane) (PDMS) and poly(dimethylsiloxane-ran-methylphenyl-siloxane) (COP)) - we have studied the morphology and the shear thinning behavior in more detail[^196]. The addition of rising amounts of the minority component creates deformable droplets or threads and the extent of shear thinning increases up to a summit, which marks the entrance into a region of co-continuity. Within that range the system becomes less susceptible to shear thinning until a minimum is reached at the composition of phase inversion.

Another related study[^267] with the same system has shown the following: If the shear rate is abruptly reduced to a preselected value and coalescence is studied as a function of time it turns out that dead end drop radii are attained in all cases; breakup is absent. For sufficiently long shearing the drop size distributions are always unimodal, but within the early stages of coalescence they are in some cases bimodal.